Everyone should read Leo Breiman's 2001 article, Statistical Modeling: The Two Cultures. (Summary: Traditional statisticians start with a distribution. They try to identify the parameters of the distribution from data that were actually generated from it. Applied statisticians start with data. They have no idea where their data really came from and are happy to fit any model that makes good predictions.)
I think there are currently three cultures of machine learning. Different people or projects will fall in different places on this "ML simplex" depending on what they care about most. They start with something in green and attempt to get blue as a way of achieving red.
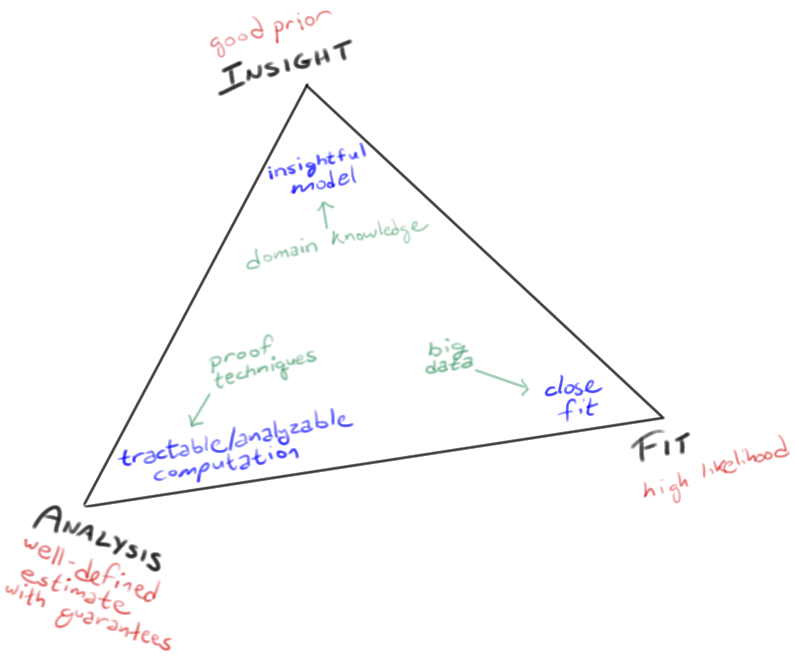
At the top of the triangle, a focus on careful domain modeling and appropriate inductive bias. This leads to exuberantly rationalist approaches because we think we know something about the data (e.g., a generative story). These "scientific" approaches are not exclusively Bayesian, but Bayesian ML practitioners cluster up here.
At the right vertex, a focus on fitting the details of the dataset. This leads to Breiman's know-nothing empiricist approach—high-capacity models like neural nets, decision forests, or nonparametrics, that will fit anything given enough data. It's assumed that the data will have unanticipated structure, which the method is to discover automatically. The human's job involves less science and more engineering (see these remarks). Deep learning people cluster here.
At the left vertex, a focus on theoretical guarantees. Estimators in the previous two cases often have to solve intractable optimization problems, which leads to approximations and local maxima: you don't know quite what you'll get. But in simple settings, the errors of both approaches can be analyzed, which gratifies the people at the left vertex. Frequentist statisticians and COLT folks (computational learning theorists) cluster around that vertex; e.g., they solve convex optimization problems and try to bound the error. Examples include spectral learning, SVMs, and other convex or closed-form frequentist estimators. For my take on the different priorities of frequentists and Bayesians, see here.
The simplex is not intended as a categorization of machine learning methods themselves. Rather, the 3 corners represent the 3 concerns that come into play when you try to choose a method: insightful modeling, model capacity, formal guarantees. Sometimes multiple concerns can be satisfied by the same method. But when they're in tension, which one do you worry about most, and which one would you soonest sacrifice? That places you on the simplex.
In practice, finding an ML attack on an applied problem usually involves combining elements of multiple traditions. It also involves using various computational tricks (MCMC, variational approximations, convex relaxations, optimization algorithms, etc.) to try to handle the maximizations and integrations that are needed for learning and inference.
(I suppose the drawing is mostly about prediction. It omits reinforcement learning and causal learning. But such problems involve prediction, so the same competing priorities guide how practitioners approach problems.)
Update: Mark Tygert alerted me that Efron (1998) gave a similar simplex diagram -- Fig. 8, "A barycentric picture of modern statistical research" -- whose corners were the Bayesian, frequentist and Fisherian philosophies.
http://cs.jhu.edu/~jason/tutorials/ml-simplex
| Jason Eisner - jason@cs.jhu.edu (suggestions welcome) | Last Mod $Date: 2016/02/03 06:33:40 $ |