Deep Marching Tetrahedra: a Hybrid Representation for High-Resolution 3D Shape Synthesis#
Authors: Tianchang Shen, Jun Gao, Kangxue Yin, Ming-Yu Liu, Sanja Fidler
Affiliations: NVIDIA, University of Toronto, Vector Institute
NeurIPS 2021
Links: PDF, Project Page
Summary#
Key Ideas#
3D Representation#
A shape is represented with a signed distance function (SDF) encoded with a deformable tetrahedral grid [1]. The grid fully tetrahedralizes a unit cube, where each cell is a tetrahedron with 4 vertices and faces. Moreover, the grid vertices can deform to represent the geometry of the shape more efficiently. The use of SDF, instead of occupancy values [1], provides more flexibility in representing the underlying surface.
Deformable tetrahedral mesh. The deformable tetrahedral mesh is denoted with
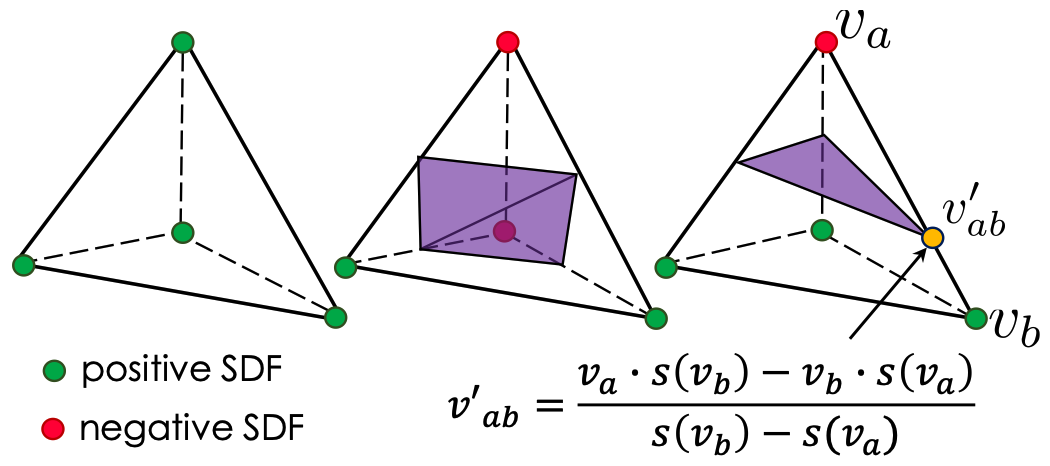
Volume subdivision. Shapes are represented in a coarse to fine manner for efficiency. Surface tetrahedra are defined as those with vertices of different SDF signs. We subdivide surface tetrahedra, as well as their immediate neighbors, by adding a mid point to each edge.
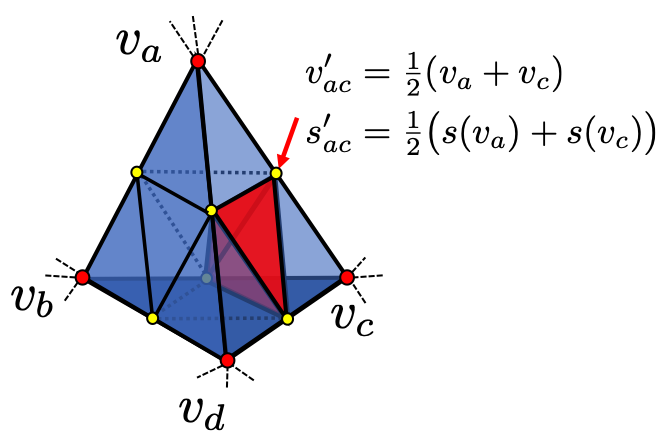
Marching tetrahedra for converting between an implicit and explicit representation. We use Marching Tetrahedra [2] to convert the SDF into an explicit triangular mesh. Based on the signs of the SDF values, MT determines the surface typology inside the tetrahedron. Once the surface typology is identified, the vertex location of the iso-surface is computed at the zero corssings of the linear interpolation along the tetrahedron’s edges.
Surface subdivision. Having a surface mesh as output allows us to increase the representation power and the visual quality with a differentiable subdivision module. The authors follow the Loop Subdivision method [3,4] and used a fixed set of learnable parameters, including positions
DMTet#
DMTet is a neural network that utilizes the proposed 3D representation and aims to output a high resolution 3D mesh
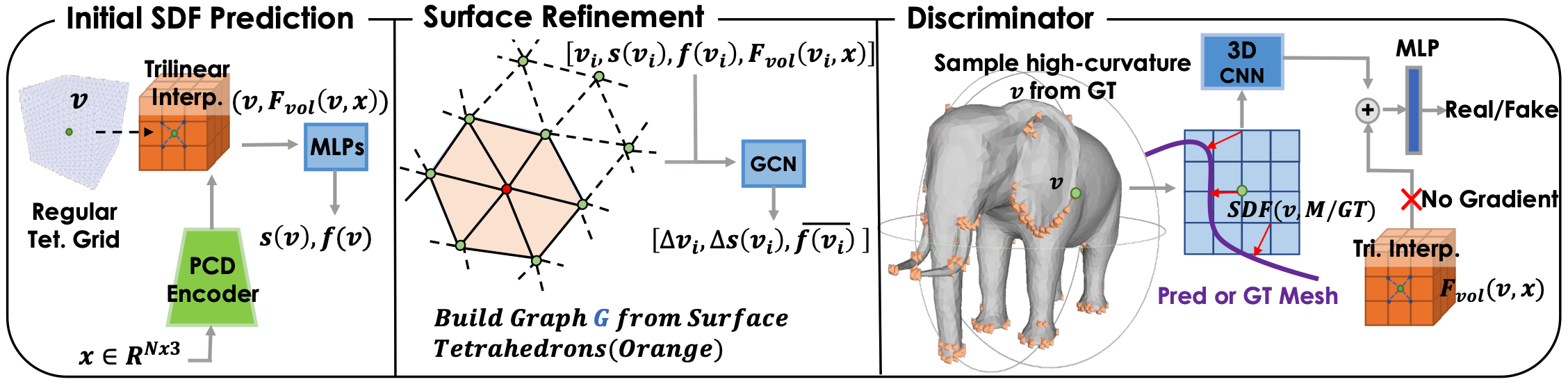
3D generator. We first use PVCNN [5] to extract a feature volume
3D discriminator. The authors empiricially found that using a 3D CNN from DECOR-GAN [6] on the SDF is effective to capture the local details. We first select a high-curvature vertex
Loss function.
Surface alignment loss. A set of points is sampled from the ground-truth and predicted mesh,
Adversarial loss. The adversarial loss
Regularizations. A SDF loss
Technical Details#
Notes#
References#
[1] J. Gao, W. Chen, T. Xiang, C. Tsang, A. Jacobson, M. McGuire, and S. Fidler. Learning deformable tetrahedral meshes for 3d reconstruction. In NeurIPS, 2020.
[2] A. Doi and A. Koide. An efficient method of triangulating equi-valued surfaces by using tetrahedral cells. IEICE TRANSACTIONS on Information and Systems, 1991.
[3] Charles Loop. Smooth subdivision surfaces based on triangles. January 1987.
[4] H. Liu, V. Kim, S. Chaudhuri, N. Aigerman, and A. Jacobson. Neural subdivision. ACM Trans. Graph., 2020.
[5] Z. Liu, H. Tang, Y. Lin, and S. Han. Point-voxel cnn for efficient 3d deep learning. In NeurIPS, 2019.
[6] Z. Chen, V. Kim, M Fisher, N. Aigerman, H. Zhang, and S. Chaudhuri. Decor-gan: 3d shape detailization by conditional refinement. In CVPR, 2021.
[7] X. Mao, Q. Li, H. Xie, R. Lau, Z. Wang, and S. Smolley. Least squares generative adversarial networks. In ICCV, 2017.